Appendix

The derivation of the segment-specific readnoise variance (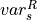{ var^R_{s} }) is shown here. This pertains to both the ‘conventional’ and ‘weighted’ readnoise variances - the only difference being the number of groups in the segment. This derivation follows the standard procedure for fitting data to a straight line, such as in chapter 15 of Numerical Recipes. 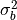The segment-specific variance from read noise corresponds to {\sigma_b^2} in section 15.2.

For read noise R, weight w = 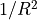{1 / R^2}, which is a constant.

n = number of groups (ngroups in the text)

t = group time (tgroup in the text)

x = starting time for each group, = 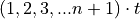{(1,2,3, ... n+1) \cdot t}

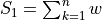
{S_1 = \sum_{k=1}^n w}

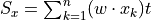
{S_x = \sum_{k=1}^n (w \cdot x_k) t}

Sxx = 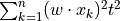{\sum_{k=1}^n (w \cd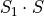ot x_k)^2 t^2}

D = {S_1 \cdot S}xx- {S_x^2}

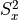
Summations needed:

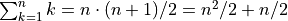
{\sum_{k=1}^n k = n \cdot (n+1) / 2 = n^2 /2 + n/2 }

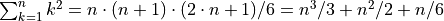
{\sum_{k=1}^n k^2= n \cdot (n+1) \cdot (2 \cdot n+1) / 6 = n^3/3 + n^2/2 +n/6 }

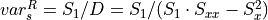
The variance due to read noise = {var^R_{s} = S_1 / D = S_1 / (S_1 \cdot S_{xx} - S_x^2)}

= { \dfrac {w \cdot n} { [w \cdot n \cdot \sum_{k=1}^n (w \cdot x_k^2 \cdot t^2)] - [\sum_{k=1}^n (w \cdot x_k \cdot t)] ^2}}

= { \dfrac {n} { w \cdot t^2 \cdot [ n \cdot ( n^3/3 + n^2/2 +n/6 ) - (n^2/2 + n/2 )^2 ] }}

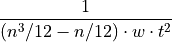
= { \dfrac {1} { ( n^3/12 - n/12 ) \cdot w \cdot t^2 }}

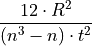
= { \dfrac{12 \cdot R^2} {(n^3 - n) \cdot t^2}}

This is the equation used in the step code and listed in the segment-specific computations section of the step Description.